Poisson random number generation

In the birdnest simulator, I use Poisson random numbers a great deal. In fact, given n individuals, each generation t must generate n Poisson random numbers. This is exceeded only by the number of uniform random numbers, for which I use TinyMT. The simplest Poisson generator is Knuth's method:

size_t
poisson_small(void *mt, float l)
{
    float     L, p;
    size_t    k;
    L = expf(-l);
    k = 0;
    p = 1.0;
    do {
        k++;
        p *= random_unit(mt);
    } while (p > L);
    return(k - 1);
}

Unforunately, this scales linearly with mean λ. Since the simulation model is intended to work with λ → ∞, and even in practise one sees λ > 30, this is unacceptable. I then ported John Cook's implementation of Atkinson's rejection method, built for values λ > 30.

size_t
poisson_large(void *mt, float l)
{
    const double c = 0.767 - 3.36 / l,
        beta = M_PI / sqrtf(3.0 * l),
        alpha = beta * l,
        k = logf(c) - l - logf(beta);
    float    u, x, v, y, temp, lhs, rhs;
    int      n;
    for (;;) {
        u = random_unit(mt);
        x = (alpha - logf((1.0 - u)/u))/beta;
        n = (int)floorf(x + 0.5);
        if (n < 0)
            continue;
        v = random_unit(mt);
        y = alpha - beta * x;
            temp = 1.0 + expf(y);
        lhs = y + logf(v/(temp*temp));
        rhs = k + n*logf(l) - log_factorial(n);
        if (lhs <= rhs)
            return(n);
    }
}

While faster than Knuth for large values of λ, sublinear performance gains were met at λ high enough to be unreasonably costly to compute. In other words, although faster, the wall-clock time of computing such high values of λ makes it unacceptable. I use Cook's Stirling's approximation to compute log_factorial().

Solutions

The simulator computes Poisson means from a payoff matrix, so one can explicitly bound values of λ from the maximum of this matrix. Since I know I have a fixed bound, and that Poisson means are natural numbers, I can precompute distributions from the finite set of possible means. To do so, I use the Poisson probability mass function (PMF), (λ^ke^-λ)/k!.

struct cache {
    float     l;
    size_t    bucketsz;
    size_t    buckets[CACHE_BUCKETS];
};

size_t
poisson_cached(void *mt, float l)
{
    static struct cache *c;
    uint32_t         key, hash;
    size_t           mmax, i, j, k;
    float            v, a, b;
    if (0.0 == l)
        return(0);
    if (NULL == c)
        c = xcalloc(CACHE_SIZE,sizeof(struct cache));
    hash = (uint32_t)l;
    key = hash % CACHE_SIZE;
    if (l != c[key].l) {
        c[key].l = l;
        k = i = 0;
        while (k < CACHE_BUCKETS) {
            a = i * logf(l);
            b = -l;
            v = a + b - log_factorial(i);
            mmax = expf(v) * CACHE_BUCKETS;
            for (j = 0; j < mmax; j++, k++) 
                c[key].buckets[k] = i;
            if (i++ > hash && 0 == mmax)
                break;
        }
        c[key].bucketsz = k;
    }
    return(c[key].buckets[random_uint
        (mt, c[key].bucketsz)]);
}

I fill m buckets with m Pr(X = x) of a given number x. To compute a Poisson number, one accesses bucket mx, where x is a uniform random number in the unit interval. I compute the natural logarithm of the PMF, and thus the log factorial, instead of doing so directly to avoid computing factorials. I can then reuse Cook's efficient log_factorial() function.

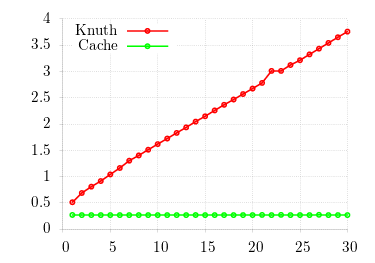
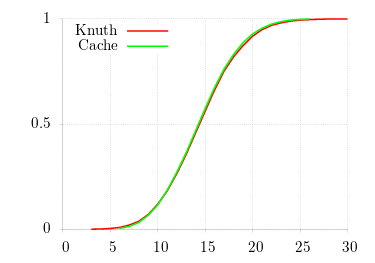
For correctness, I fix λ = 15 and show the CDF (using gnuplot's cumulative smoothing function) for 10⁴ samples. One can see the constant-time access of the cache algorithm as well as the accuracy of its results.